Projection Matrixについて
はじめに
Projection Matrixは何となくややこしいイメージが強い。実際ややこしい。自分でも勘違いすることがある。 なのでいったんまとめることにする。
Row Major, Column Major, ベクトルとの乗算の順序
Projection Matrixは4x4の正方行列で、メモリに格納するときに行要素を優先して格納すればRow-Major、列要素を優先して格納すればColumn-Majorと呼ばれる。
Row-Majorは以下の添え字の順番で格納したものを指す。
$$ \begin{pmatrix} a_1 & a_2 & a_3 & a_4 \\ a_5 & a_6 & a_7 & a_8 \\ a_9 & a_{10} & a_{11} & a_{12} \\ a_{13} & a_{14} & a_{15} & a_{16} \end{pmatrix} $$
対してColumn-Majorは、以下の添え字の順番で格納したものを指す。
\begin{pmatrix} a_1 & a_5 & a_9 & a_{13} \\ a_2 & a_6 & a_{10} & a_{14} \\ a_3 & a_7 & a_{11} & a_{15} \\ a_4 & a_8 & a_{12} & a_{16} \end{pmatrix}
また、行列の積は可換ではない。たとえば、4次元ベクトルを行列の右から掛けるか左から掛けるかによって演算が変わるので、これには2通りの演算が存在する。
$$
\begin{pmatrix} x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ w^{\prime} \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ w \end{pmatrix}
$$
$$ \begin{pmatrix} x^{\prime} & y^{\prime} & z^{\prime} & w^{\prime} \end{pmatrix} = \begin{pmatrix} x & y & z & w \end{pmatrix} \begin{pmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{pmatrix} $$
シェーダーを記述する場合は、これらの解釈は実装者に委ねられる。一方で、グラフィックスAPIがこれらの演算を提供する場合もある。 OpenGLのCompatibility Profileでは、Column-Majorでマトリクスをメモリに格納し、Projection Matrixとの乗算はベクトルに対して左側からである。 Direct3D 9では、Row-Majorでマトリクスをメモリに格納し、Projection Matrixとの乗算は、ベクトルに対して右側からである。
座標変換の過程について
次に座標変換の過程について簡単に説明する。頂点シェーダーが出力する4次元ベクトルは、一般的にはView座標系の位置にProjection Matrixを乗算した結果が出力される。 この座標は同次座標と呼ばれ、W成分で(X,Y,Z)を除算して正規化することで、Normalized Device Coordinate(正規化デバイス座標系)に変換される(Perspective Division)。次にViewport変換を行い、Normalized Device Coordinateを、描画用のバッファ(スクリーン)の領域にマッピングする。 多少の用語の違いがあるが、OpenGL、Vulkan、Direct3Dの3つのグラフィックスAPIは概ね同じ座標変換のステップを持っている。ただし各APIごとに座標軸の考え方や値の範囲が異なるので注意が必要である。
Y軸の反転について
一般的に3D空間上ではY軸を上向きと考える事が多い一方で、2Dスクリーン上では、ピクセルデータを画像の左上から格納する事が多い関係上、Y軸は下向きと考えることが多い。そのため、Projection Matrixによる投影変換、Perspective Division、そしてViewport変換の過程においてY軸を反転させることがある。ここではこれについて説明する。各種変換や用語に関する解説と前後するが、先にここにまとめておく。
OpenGL
OpenGLでは、元来Y軸の反転を行わないという思想の基にAPIが設計されていた。したがって、Viewport変換後のWindow座標系では、画像の左下を原点としてピクセルデータを取り扱う。そのため、Framebufferを画像として表示するときは垂直方向でデータを反転させて表示させるのが一般的である。しかし、現在のOpenGLでは、glClipControl()でGL_UPPER_LEFTを設定すると、Perspective Divisionの際にY軸の符号を反転させる。これによって、Normalized Device CoordinateのY軸の上下が反転するので、Framebufferのデータが画像の左上を原点として格納されるようになる。Perspective Divisionについては、 OpenGL 4.6 Core Pprofileの13.8に記載がある。
Direct3D
Direct3Dの座標変換に関しては、 このドキュメントに記述がある。これによれば、Perspective DivisionはViewport変換のスケーリングの後に行われており、Y軸の符号反転は、Viewportのスケーリングの係数の符号を逆転し、オフセットを調整することで実装されている。 また、 他のドキュメントでも、Normalized Device CoordinateのY軸はView座標系と同じ向きに描写されている。したがって、Direct3DではViewport変換でY軸の符号の反転が行われていると解釈できる。 Viewport変換後のScreen座標系では、画像の左上を原点としてピクセルデータを取り扱う。
Vlukan
Vulkan 1.2によれば、Perspective DivisionでY軸の符号を反転しない。また、Viewport変換時もY軸の符号を反転しない。そして、Viewport変換後のFramebuffer Coordinateの原点は、左上とされている。そのため、VulkanではProjection Matrixの演算でY軸を反転しない限り、Y軸を上向きとする空間を投影変換した像は上下が反転する。 また、Framebuffer Coordinateとの関連性を考えれば、VulkanのNormalized Device CoordinateのY軸は下向きと考えるのが自然である。
Perspective Division
Projection Matrixとの演算を終えた4次元ベクトルは、同次座標を表現する。これを正規化する($w=1$にする)作業は、プログラムなどで制御ができない固定された機能として、グラフィックスAPI側が行う作業となっている。 デフォルトの設定のOpenGL, Vulkan, Direct3Dでは、単純な$w$による除算が行われる。 $$ \begin{pmatrix} x_d \\ y_d \\ z_d \end{pmatrix} = \begin{pmatrix} \frac{x_v}{w_v} \\ \frac{y_v}{w_v} \\ \frac{z_v}{w_v} \end{pmatrix} $$
ただし、OpenGLでglClipControl()でGL_UPPER_LEFTが設定されているときは、Perspective Divisionの実行時に$Y$の符号が逆転される。 これは、3D空間上ではY軸を上向きと考えることが一般的である一方、画像フォーマットや、Microsoft Windows や X Window Systemでは、 垂直方向は画面の上から下に向かって座標軸を考えることが多いため、座標軸の向きを入れ替えるための計算である。 $$ \begin{pmatrix} x_d \\ y_d \\ z_d \end{pmatrix} = \begin{pmatrix} \frac{x_v}{w_v} \\ -\frac{y_v}{w_v} \\ \frac{z_v}{w_v} \end{pmatrix} $$
正規化された後の(X,Y,Z)はNormalized Device Coordinate(正規化デバイス座標系)を表現する
Normalized Device Coordinate (NDC)
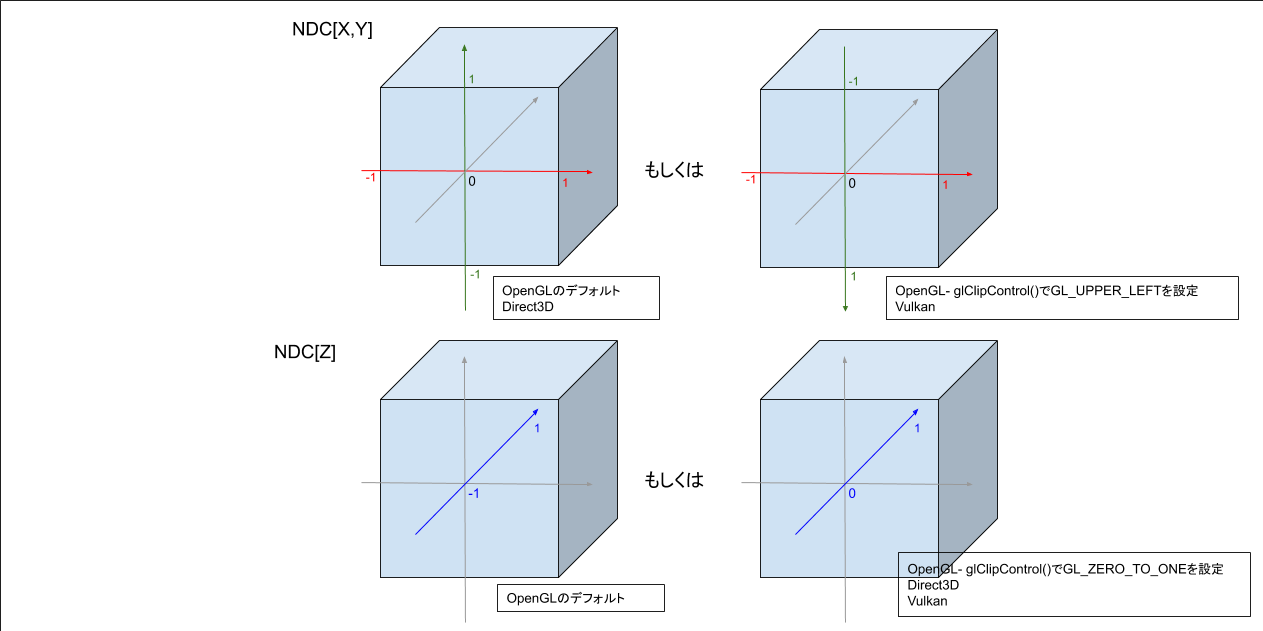
NDCは、シェーダーコードが出力した同次座標を、Perspective Divitionにより正規化した後の座標系となる。この座標系は$X,Y$は範囲が[-1, 1]と決まっており、 $Z$は[-1, 1]あるいは[0,1]と決まっている。この座標系は、$X,Y$はRenderTargetピクセル位置を表すスクリーン座標系と線形の関係にある。$Z$は深度バッファの値と線形の関係にある。
OpenGLでは、glClipControl()でNDCのZ軸の範囲を[-1, 1]か[0, 1]のどちらかで選択することができる。デフォルトでは、GL_NEGATIVE_ONE_TO_ONE[-1, 1]が設定されており、GL_ZERO_TO_ONE[0, 1]を設定することで、Direct3D/Vulkanと同じ範囲になる。また、glClipControl()でGL_UPPER_LEFTを設定すると、Perspective DivisionでY軸の符号が反転されるので、NDCのY軸が反転する。
Viewport変換
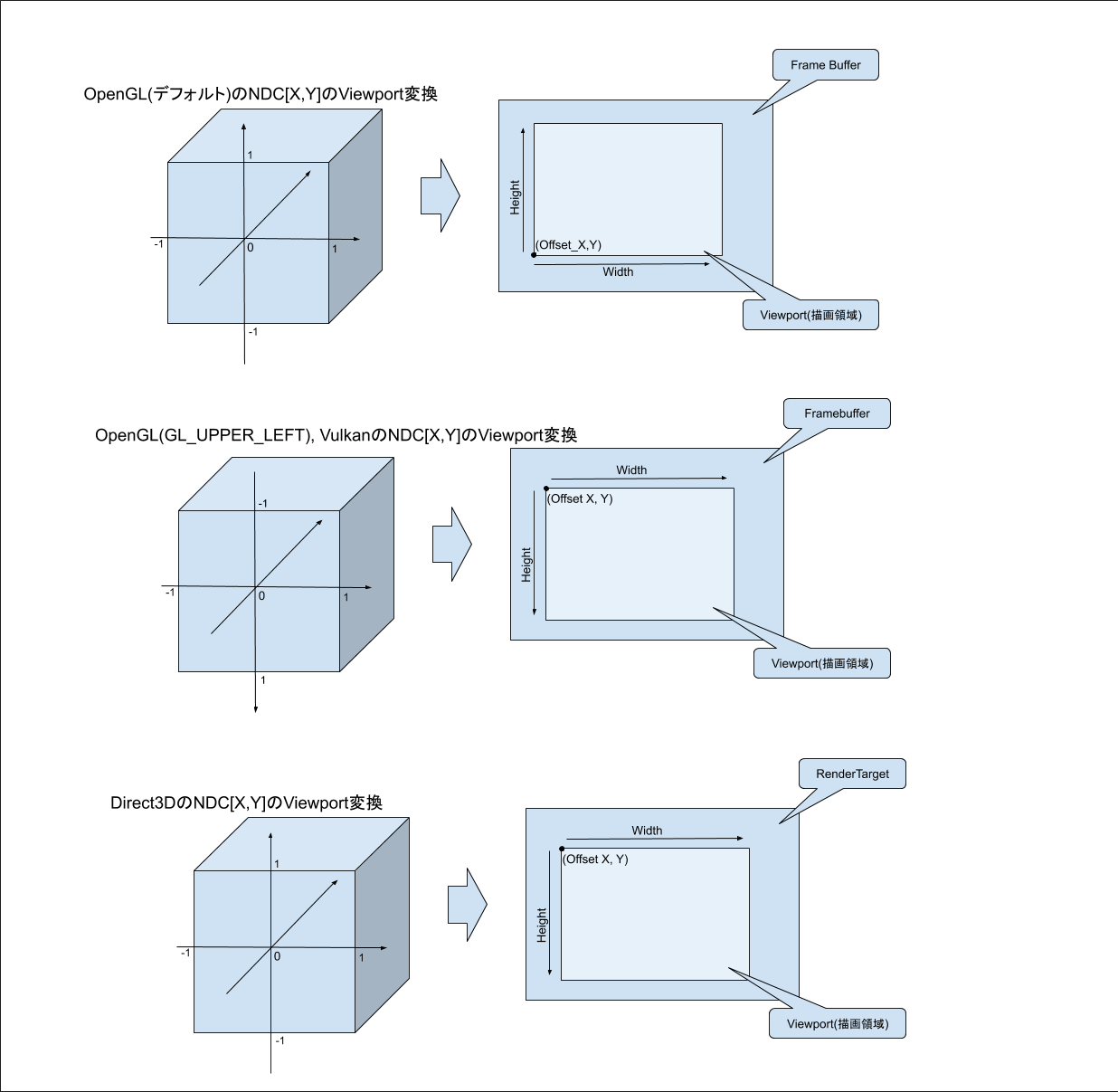
NDCにおける$X,Y$の値の範囲は[-1, 1]だが、これをViewport変換によりRenderTargetのピクセル位置を表すスクリーン座標系に線形にマッピングする。RnederTarget上でのオフセットと幅と高さを指定する事でViewport変換が実現される。 一般的には、オフセットをゼロに設定し、幅と高さをRenderTargetの幅と高さとすることで、NDCの$X,Y$の[-1, 1]の範囲をRenderTargetの全ピクセルにマッピングすることが多いが、描画領域を分けて複数のViewportのレンダリング結果を一枚のRenderTargetにレンダリングする事もある。
Direct3DはViewport変換時にY軸の上下が入れ替わるように計算される。
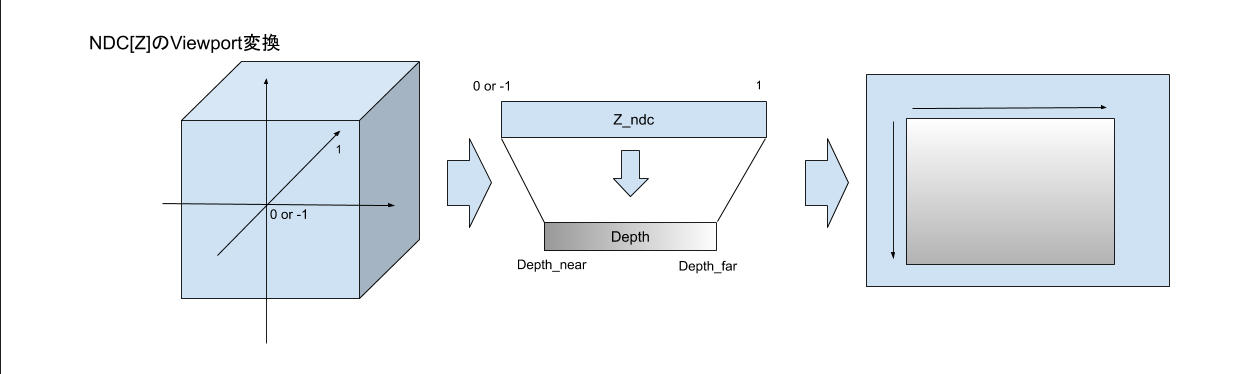
$Z$に関しては、Viewport変換後の深度値の値の範囲を$near, far$の二つの値で指定し、範囲は[0, 1]に収まる様にしなくてはならない。Viewportの$near, far$は深度バッファで使用する値の範囲の事で、 Projection Matrixの$near, far$とは全く意味が異なる。ほとんどの場合では、[0, 1]を指定して、深度バッファが表現できる全ての範囲を使用する。 OpenGLは、NDCのZの範囲を[-1, 1]としているときは、必ずViewport変換時に[near, far]への線形変換が行われる。対して、NDCの範囲が[0, 1]の場合は、Viewport変換の$near, far$が、[0, 1]に設定されている場合は、NDCの$Z$の値がそのまま深度バッファの値として格納される。
右手系、左手系
右手系、左手系とは、単位マトリクスのX,Y,Z軸の各ベクトルの、認識している空間におけるマッピングである。右手系は、右手の(親指,人差し指, 中指)を自然な形で直交させたとき、(X, Y, Z)の向きとなる空間を指す。 左手系も同様である。デフォルトのOpenGLとDirect3DのNDCは、はX軸が画面左から右、Y軸が画面下から上、Z軸が画面手前から奥なので、左手系である。 一方で、glClipControl()でGL_UPPER_LEFTを設定したOpenGLとVulkanのNDCは、X軸が画面左から右、Y軸が画面上から下、Z軸が画面手前から奥なので、右手系である。
よく耳にする話として、OpenGLが右手系でDirect3Dが左手系という話があるが、OpenGLに関してはglFrustum()/glOrtho()という関数が、 右手系のViewMatrixの-Z方向を、左手系のNDCの+Z方向として変換するためのProjection Matrixを計算することに起因している。 実際にはProjection MatixにはglLoadMatrixで自由に値を設定することができるので、OpenGLは元来シェーダーを使わなくても、右手系でも左手系でも自在に描画できるはずである。 また、Direct3DにはProjection Matrixを計算するAPIは用意されていない。ただし、ユーティリティ関数群のD3DXには、D3DXMatrixPerspectiveRH()という関数が用意されている。 この関数は右手系ViewMatrixの-Z方向を、左手系のNDCの+Z方向として変換するProjection Matrixを計算する。同様に、D3DXMatrixPerspectiveLH()という関数も用意されており、 こちらは、左手系のViewMatrixの+Z方向を、左手系のNDCの+Z方向として変換するProjection Matrixを計算する。
このように、ある特定のグラフィックスAPIの座標系が右手系左手系のいずれかに属していると考えること自体が誤りだといえる。
Projection Matrixの役割
さて、ここからが本題ののProjection Matrixに関する説明になる。View座標系からNDC座標系への変換を担うProjection Matrixには、主に4つの要素がある。
- Y軸の向きの入れ替え (Vulkan)
- Z軸の向きの入れ替え
- X,Y軸に関する透視投影変換
- Z軸のNDC座標へのマッピング
透視投影変換を行わない正射影というProjection Matrixもあるが、ここでは割愛する。
Y軸の向きの入れ替え (Vulkan)
Vulkan特有の事なので一番最初に解説する。Vulkanは先に説明した通り、NDCのY軸は下向きでPerspective DivisionやViewport変換でY軸の符号反転を行わない。 したがって、Y軸が下向きとなる様に頂点シェーダーの出力を行わなければならない。そのため、View座標系でY軸が上向きになるように座標を扱っていた場合、Projection MatrixでY軸を反転させる必要がある。 具体的にはProjection Matrixの、Y成分のスケーリングとオフセットを担当する成分(以下の場合では$a_{22}, a_{23}$)の符号を入れ替える事で、NDCの上下が反転した結果を得る事ができる。
$$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & -a_{22} & -a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$
Z軸の向きの入れ替え
同次座標の$w$は、単にPerspective Divisionでの除算に使われるだけでなく、ポリゴン平面上の属性値補間でPerspective Correctionを行うときに使用されるので、$Z$軸に沿って正しく透視投影変換をするときは下記のどちらかの設定になる。
- $Z_{View}$の正の方向にNDCのZ軸を取る場合は、Projection Matrixを乗算した後の同次座標の$w$に、$Z_{View}$が格納されるようにしなければならない。
そのため、$Z_{View}$と乗算される位置に$1$を設定する。 - $Z_{View}$の負の方向にNDCのZ軸を取る場合は、Projection Matrixを乗算した後の同次座標の$w$に、$-Z_{View}$が格納されるようにしなければならない。
そのために$Z_{View}$と乗算される位置に$-1$を設定する。
以下は、それぞれ$Z_{View}$正負の方向にNDCのZ軸を設定し、透視投影変換をする場合のProjection Matrixである。殆どのProjection Matrixは下記のいずれかである。 余談だが、この、$w$と乗算される行(あるいは列)は特徴的なので、これを手がかりに、メモリにダンプされたマトリクスが、Row-MajorなのかColumn-Majorなのかを簡単に見分ける事ができる。
$$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$ $$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ 0 & 0 & -1 & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$
X,Y軸に関する透視投影変換
透視投影変換は、空間にある物体が視点から離れる程小さく投影される様に変換する役割がある。これにより遠近感が演出される。 視点からの距離が二倍になれば、物体は長さで二分の一の大きさで描画されるようにする。したがって$Z$軸向きに透視投影した$X,Y$座標は、$1/Z$に比例する。
$X,Y$軸に関する透視投影変換は、つまるところ、以下の式の$a, b, c, d$を決定することにある。 $$ X_{NDC} = \frac{a * X_{View}}{Z_{View}} + b $$ $$ Y_{NDC} = \frac{c * Y_{View}}{Z_{View}} + d $$
$a, c$の値が、水平、垂直視野角を決定し、$b, d$がView座標系からNDC座標系に変換するときのオフセットになる。$b, d$は、View座標のZ軸がNDC座標のX,Yの中心を通る場合はゼロになる。
水平、垂直視野角から$a,c$の値を計算する場合は、視野の両端がNDCにおける[-1, 1]になるように計算すれば良い。
もう一つの、係数$a,c$の計算方法として、$Z_{View}=near$平面上での視野の上下左右に相当する$left, right, top, bottom$を指定する方法である。以下の図には$left, right$による水平視野角を示す。
上図はView座標系での、$Z_{View}=near$平面上でのオフセット値になるので、NDC座標系に変換するには、$2/(r-l)$を乗算する必要がある。したがって、オフセットの値は以下の様になる。 $$b = -\frac{r+l}{r-l}$$ $$d = -\frac{t+b}{t-b}$$ オフセットの値は、NDC座標系において一定なので、View座標系においては$Z_{View}$の値に比例する。
また、オフセットがない場合は、$near, left, right, top, bottom$と$\theta, \phi$に、以下のような関係が成り立つ。 $$ l = n \cdot tan(\frac{\theta}{2}) $$ $$ r = -n \cdot tan(\frac{\theta}{2}) $$ $$ t = n \cdot tan(\frac{\phi}{2}) $$ $$ b = -n \cdot tan(\frac{\phi}{2}) $$
次に、Projection Matrixへの各係数の設定だが、$a, c$の値は、それぞれ$X_{View}$, $Y_{View}$と乗算されるように格納する。$Z_{View}$の除算の部分はPerspective Divisionで行われる。 $b, d$の値は、$Z_{View}$と乗算されるようにProjection Matrixに格納する。これは、のちにPerspective Divisionで相殺されることでオフセット値として機能する。 $$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} \frac{1}{tan(\frac{\theta}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{tan(\frac{\phi}{2})} & 0 & 0 \\ a_{31} & a_{32} & a_{33} & a_{34} \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$
以下のマトリクスはD3DXMatrixPerspectiveOffCenterLHが算出する係数と符合する。 $$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} \frac{2n}{r - l} & 0 & -\frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0 \\ a_{31} & a_{32} & a_{33} & a_{34} \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$
一方で、Z軸の向きの入れ替えるために、$a_{43}$に$-1$を設定している場合は、$Z_{View}$が乗算される時と、除算される時で符号が異なるため、オフセットの係数の符号が変わる。 以下のマトリクスはD3DXMatrixPerspectiveOffCenterRHが算出する係数や、glFrustum()が算出する係数と符合する。 $$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} \frac{2n}{r - l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ a_{31} & a_{32} & a_{33} & a_{34} \\ 0 & 0 & -1 & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$
Z軸のNDC座標へのマッピング
Z軸に関する変換は透視変換ではなく、Z軸の値の一定の範囲をNDCで許されている値の範囲に、大小関係を損なわずに変換することである。通常は、View座標系の広大なZ軸の範囲を、NDCで許されている高々[0, 1]程度の範囲にマッピングする圧縮作業である。 簡単に考えれば、View座標系のZの値にオフセットとスケールを適用すれば実現できるが、これは残念ながら推奨されない。 $$Z_{NDC} = e * Z_{View} + f$$
- 一つ目の理由は、Projection Matrixを使った座標変換による制限によるものである。$X, Y$の値を透視投影変換するためには、同次座標系の$W$の値を$Z$(もしくは$-Z$)の値としなければ、$X,Y$軸に関する透視投影変換が実現できない。そのため$W$の値は決定されていると言える。 この条件では、Projection Matrixとの乗算では、View座標系の$Z$と1次比例の関係を作ることができない。一応ながら、Pixel Shader内で深度バッファに出力する値を直接計算することで実現可能だが、GPUの早期Zカリング機能が無効化されるので実際のアプリケーションの運用では現実的な方法とは言えない。
- 二つ目の理由は、透視投影変換後のNDCでの$X,Y$平面(つまりはスクリーンスペース)では、$Z_{View}$は線形性を失う。代わりに$1/Z_{View}$が線形性を持つことになる。 投影変換されたポリゴン平面の深度値を高速に計算するならば、線形性を失った$Z_{View}$に比例した式で計算された値は単純な補間では計算出来ず、計算コストが高く効率が良くない。それよりも、大小関係を(反転しつつも)保ちつつ、スクリーンスペースで線形性を持つ$1/Z_{View}$を使う方が合理的だったという経緯がある。 (ちなみに、スクリーンスペースでテクスチャのU,Vなどの頂点属性値は、$attribute/W$と$1/W$をスクリーンスペースで線形補間し、その結果を除算することで補完された頂点属性値を計算している。)
したがって、一般的にGPUでは$Z_{View}$ではなく$1/Z_{View}$を線形変換した結果をNDCのZ座標として採用している。 $$Z_{NDC} = \frac{e}{Z_{View}} + f$$
また、このようにすると、深度バッファに整数の格納フォーマットを使った場合、$Z$の値が小さいときほど、多くのBitを使って表現することになる。 つまり、近くの物体ほど深度バッファの多くのBitが割り当てられるので、これは合理的であるとも考える事ができる。また、$1/Z$の線形変換であれば、Projection Matixで一元的に扱えるのも利点である。
係数$e, f$の決定は、View座標系における、Z軸の範囲である$near, far$の値が、[0, 1] (もしくは[-1, 1])になるように連立方程式を解くだけで計算できる。
NDC[0, 1]の場合
下記の式を解けば、D3DXMatrixPerspectiveFovLHに設定される係数と符合する。
$$1 = \frac{e}{far} + f$$ $$0 = \frac{e}{near} + f$$ $$1 = e (\frac{1}{far} - \frac{1}{near})$$ $$e = -\frac{far \cdot near}{far-near}$$ $$f = \frac{far}{far - near}$$
Projection Matrixに設定するときは、$Z_{View}$と乗算される位置に$f$を設定し、$W$(通常は1.0)と乗算される方に$e$を設定する。Perspective Divisionで$W$(この時点では$Z_{View}$)による除算が行われ、上記の式と等価な計算が行われる。
$$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} \frac{1}{tan(\frac{\theta}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{tan(\frac{\phi}{2})} & 0 & 0 \\ 0 & 0 & \frac{far}{far - near} & -\frac{far \cdot near}{far-near} \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$
Z軸の向きを反転させる場合は、Projection Matrixの乗算をよく観察する必要がある。$1/Z_{View}$の係数である$e$は、$W_{View}$と乗算して、$-Z_{View}$で除算される。$W_{View}$は通常$1.0$で$-Z_{View}$も正の数なので、上記で求めた$e$がそのまま使える。 一方で、オフセットの$f$は、$Z_{View}$と乗算して、$-Z_{View}$で除算される。したがって、上記で求めたものの符号を反転させたものを使う必要がある。こうして求めた結果は、D3DXMatrixPerspectiveFovRHの係数と符合する。
$$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} \frac{1}{tan(\frac{\theta}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{tan(\frac{\phi}{2})} & 0 & 0 \\ 0 & 0 & \frac{far}{near-far} & \frac{far \cdot near}{near -far} \\ 0 & 0 & -1 & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$
NDC[-1, 1]の場合
上記と同様の手順で係数$e, f$を求める事ができる
$$1 = \frac{e}{far} + f$$ $$-1 = \frac{e}{near} + f$$ $$2 = e (\frac{1}{far} - \frac{1}{near})$$ $$e = -\frac{2(far \cdot near)}{far-near}$$ $$f = \frac{far + near}{far - near}$$
それぞれをProjection Matrixに設定すると以下の様になる。
$$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} \frac{1}{tan(\frac{\theta}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{tan(\frac{\phi}{2})} & 0 & 0 \\ 0 & 0 & \frac{far + near}{far - near} & -\frac{2(far \cdot near)}{far-near} \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$
Z軸の向きを反転させる場合も先ほどと同様の手順となる。これはglFrustum()関数の係数と符合する。
$$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} \frac{1}{tan(\frac{\theta}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{tan(\frac{\phi}{2})} & 0 & 0 \\ 0 & 0 & -\frac{far + near}{far - near} & -\frac{2(far \cdot near)}{far-near} \\ 0 & 0 & -1 & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$
Inverse Z
深度バッファに浮動小数点の格納フォーマットが使えるとき、NDCにおける深度のマッピングを、[Near, Far]を[0, 1]ではなく[1, 0]にマッピングすることで、$far$付近での深度バッファの精度不足を解消することができる。
NDCが[-1, 1]の場合や、深度バッファの格納フォーマットが整数表現の場合は、Inverse Zを使う利点はない。
精度については詳しくは以下に解説がある。
Depth Precision - Nathan Reed
NDC[1, 0]の場合
Inverse Zの設定は簡単で、先ほどの連立方程式の$near$と$far$を入れ替えて解くだけで係数は求まる。レンダリングの際には、深度バッファのクリア値を、1ではなく0に設定し、ラスタライザーの深度テストの条件を反転させればよい。 $$1 = \frac{e}{near} + f$$ $$0 = \frac{e}{far} + f$$ $$e = \frac{far \cdot near}{far - near}$$ $$f = -\frac{near}{far-near}$$
$$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} \frac{1}{tan(\frac{\theta}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{tan(\frac{\phi}{2})} & 0 & 0 \\ 0 & 0 & -\frac{near}{far-near} & \frac{far \cdot near}{far - near} \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$ $$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} \frac{1}{tan(\frac{\theta}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{tan(\frac{\phi}{2})} & 0 & 0 \\ 0 & 0 & \frac{near}{far-near} & \frac{far \cdot near}{far - near} \\ 0 & 0 & -1 & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$
Infinite Far Plane
$far$を無限遠に設定する事で、Far Clippingを実質無効化するとともに、浮動小数点の丸め誤差を低減することができる。Projection Matrixに設定する係数の計算は、今まで求めてきた係数の、$far$を無限大で極限を取れば算出される。 Infinite Far Planeのメリットは、非常に遠くのオブジェクトを描画してもクリッピングされることがないことと共に、空や星などを描画する際に、$W_{View}$をゼロとすることで、$(X_{View}, Y_{View}, Z_{View})$方向の無限遠を描画することができることである。
NDC[0, 1]の場合
$$e = \lim_{far\to\infty} -\frac{far \cdot near}{far-near} = -near$$ $$f = \lim_{far\to\infty} \frac{far}{far - near} = 1$$
Inverse Zを用いないInfinite Far Planeは、無限遠の深度値が1.0となるが、$Z_{View}$が極大化すると正確に描画できないことがあるので注意が必要である。これはProjection Matrixを使った演算とPerspective Divisionでオフセットを設定する場合に、$Z_{View}$による乗算と除算が行われるため、この値が非常に大きな値になれば、浮動小数点数としての精度を失ってしまうからである。
NDC[1, 0]の場合
一方で、Inverse Zを用いた場合のInfinite Far Planeの係数は以下の様に計算される。 $$e = \lim_{far\to\infty} \frac{far \cdot near}{far - near} = near$$ $$f = \lim_{far\to\infty} -\frac{near}{far-near} = 0$$
Inverse Zを用いたInfinite Far Planeは、オフセットの係数がゼロなので、$Z_{View}$が極大化する事によるProjection Matrixとの乗算による精度の問題を起こさない。以下は、Inverse Zを用いたInfinite Far PlaneのProjection Matrixである。$a_{43}$は$1$でも$-1$でも変わらない。 $$ \begin{pmatrix} x_d \\ y_d \\ z_d \\ w_d \end{pmatrix} = \begin{pmatrix} \frac{1}{tan(\frac{\theta}{2})} & 0 & 0 & 0 \\ 0 & \frac{1}{tan(\frac{\phi}{2})} & 0 & 0 \\ 0 & 0 & 0 & near \\ 0 & 0 & a_{43} & 0 \end{pmatrix} \begin{pmatrix} x_v \\ y_v \\ z_v \\ w_v \end{pmatrix} $$
深度バッファから$Z_{View}$の逆算
マルチパスレンダリング等を行っていると、描画された深度バッファより、$Z_{View}$を求めたい時がある。計算自体は単なる逆算なので簡単である。
深度バッファから$Z_{View}$を逆算するためには、まず、Viewport変換を逆変換して$Z_{NDC}$を計算する必要がある。Viewportの$near, far$とNDCの$Z$軸の範囲が分かれば計算は簡単である。深度バッファとNDCの範囲が一致する場合は、この計算は不要である。 $$Z_{NDC} = \frac{Depth - near_{Viewport}}{far_{Viewport} - near_{Viewport}}$$
NDC[0, 1]の場合
Projection Matrixに設定した係数$e, f$を使って$Z_{NDC}$から$Z_{View}$を逆算する。$Z_{NDC}$が正の$Z_{View}$方向ならば以下の式で計算できる。 $$Z_{NDC} = \frac{e}{Z_{View}} + f$$ $$Z_{View}= \frac{e}{Z_{NDC} - f} = \frac{far \cdot near}{far - Z_{NDC} (far - near)}$$
$Z_{NDC}$を負の$Z_{View}$方向に取っている場合は符合の操作が必要である。まず、オフセットの値$f$の符合を反転させてあるので、これを反転する必要がある。加えて$Z_{View}$は負の方向なので、最後に符合を反転する必要がある。 $$Z_{View}= - \frac{e}{Z_{NDC} + f} = -\frac{far \cdot near}{far - Z_{NDC} (far - near)}$$
NDC[1, 0]の場合
Inverse Zを用いた場合は以下の通り。 $$Z_{View}= \frac{e}{Z_{NDC} - f} = \frac{far \cdot near}{near + Z_{NDC} (far - near)}$$ Inverse Zで、$Z_{NDC}$を負の$Z_{View}$方向に取っている場合は以下の通り。 $$Z_{View}= - \frac{e}{Z_{NDC} + f} = -\frac{far \cdot near}{near + Z_{NDC} (far - near)}$$
Inverse Zを用いたInfinite Far Planeの場合は、式はもっと単純になる。ただし、$Z_{NDC}$がゼロの場合はゼロ除算になるので注意が必要である。 $$Z_{View}= \frac{e}{Z_{NDC}} = \frac{near}{Z_{NDC}}$$ $Z_{NDC}$を負の$Z_{View}$方向に取っている場合は以下の通り。 $$Z_{View}= -\frac{e}{Z_{NDC}} = -\frac{near}{Z_{NDC}}$$
NDC[-1, 1]の場合
上記と同じ手順で計算する。 Depthから$Z_{NDC}$は以下の通り。 $$Z_{NDC} = \frac{2(Depth - near_{Viewport})}{far_{Viewport} - near_{Viewport}} -1$$
$Z_{NDC}$から$Z_{View}$は以下の通り。 $$Z_{View}= \frac{e}{Z_{NDC} - f} = \frac{2 \cdot far \cdot near}{far + near - Z_{NDC} (far - near)}$$ $Z_{NDC}$を負の$Z_{View}$方向に取っている場合は $$Z_{View}= -\frac{e}{Z_{NDC} + f} = -\frac{2 \cdot far \cdot near}{far + near - Z_{NDC} (far - near)}$$
深度バッファからLinear Depthの計算
上記で示した通り、Projection MatrixのNearとFarが分かれば、深度バッファから$Z_{View}$を復元できるが、 実際には$Z_{View}$よりも、単に線形性がある深度値としてのLinear Depthが欲しいケースが多い。 ここでのLinear Depthは[near, far]が[0, 1]にマッピングされており、かつ線形性を保っているものを指す。 計算は先の式の[near, far]を[0, 1]に線形でマッピングするだけである。
NDC[0, 1]の場合
$$Z_{Linear}= \{ \frac{far \cdot near}{far - Z_{NDC} (far - near)} - near \} \frac{1}{far -near} = \frac{Z_{NDC} \cdot near}{far - Z_{NDC}(far - near)} = \frac{Z_{NDC}}{\frac{far}{near} - Z_{NDC}(\frac{far}{near}-1)} $$
NDC[1, 0]の場合
Inverse Zを用いた場合は以下の通り。[near, far]を[0, 1]にマッピングするので、Inverse Zの大小関係は再び反転するので注意。 $$Z_{Linear}= \{ \frac{far \cdot near}{near + Z_{NDC} (far - near)} - near \} \frac{1}{far -near} = \frac{near (1 - Z_{NDC})}{near + Z_{NDC}(far -near)} = \frac{1 - Z_{NDC}}{ 1 + Z_{NDC}(\frac{far}{near} - 1)}$$
Render Targetのピクセル位置から視線ベクトルの逆算
G-Buffer等を用いている場合は、Render Targetのピクセル位置から視線ベクトルを逆算したい事も多い。これも上記と同様で、Projection Matrixからの逆算で計算自体は簡単である。
Render Targetのピクセル位置から視線ベクトルの逆算するためには、Viewport変換を逆変換して$X_{NDC}, Y_{NDC}$を計算する。 $$X_{NDC} = \frac{2(X_{Pixel} - OfsX_{Viewport})}{Width_{Viewport}}-1$$ $$Y_{NDC} = \frac{2(Y_{Pixel} - OfsY_{Viewport})}{Height_{Viewport}}-1$$
また、Render Targetのピクセル位置ではなく、フルスクリーン描画したポリゴンのUV値から$X_{NDC}, Y_{NDC}$を逆算する方法も良く用いられる。いずれにせよ、範囲が明確なNDCの座標を再計算するのは簡単である。
次に$Z_{View}=1$の場合の、$X_{View}, Y_{View}$を計算する。ここでの$a,b,c,d$は、先ほど透視投影変換で求めた値で、$\theta, \phi$は水平、垂直視野角である。 $$X_{View1} = \frac{X_{NDC} - b}{a} = tan(\frac{\theta}{2})X_{NDC}$$ $$Y_{View1} = \frac{Y_{NDC} - d}{c} = tan(\frac{\phi}{2})Y_{NDC}$$
三次元ベクトル$(X_{View1}, Y_{View1}, 1)$は、View座標系の原点からピクセルへのベクトル:視線ベクトルを表すが、長さが1ではないのでライティングの計算をする場合は正規化する必要がある。 一方で、ピクセルのView座標系における位置を求める場合は、このベクトルに$Z_{View}$を乗算することで求める事ができる。
まとめ
もっと簡単にまとめたかったが、ダラダラと長くなってしまった。